3.2 Turing-Automaten und Regel-Sprachen
Um die Klasse der von Automaten akzeptierten Sprachen über die kontextfreien
Sprachen hinaus zu erweitern, heben wir die beim Kellerautomaten angenommene
Beschränkung des RAM-Speichers als Keller wieder auf und betrachten ein unendliches
Speicherband, wo an beliebigen Stellen (Zellen) gelesen und geschrieben werden
kann. Wir benutzen dazu das nach beiden Seiten offene Eingabeband. Um beliebige
Stellen dieses Bandes zu erreichen, geben wir dem Automaten die Möglichkeit,
neben dem Lese- und Schreibvorgang, ausgehend von einer Zelle die linke oder
rechte Nachbarzelle aufzusuchen. Zusammen mit dem zu schreibenden Symbol wird
diese Bewegungsmöglichkeit durch eine Ausgabereaktion des Automaten bestimmt.
Wir folgen dem von Turing (1936) vorgeschlagenen Modell des Turing-Automaten
und untersuchen die von diesem akzeptierte Sprachklasse.
 |
Definition: Turing-Automat
- Eine Struktur T = ( X, Y, Z, h, z0, F, # ) heißt Turing-Automat
, falls
- X, Y, Z nichtleere endliche Mengen, X
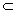 Y, Y Y, Y 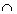 Z = Z = 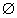 , # , #  Y \ X , Y \ X ,
z0 Z, F Z, F 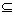 Z und Z und
- h eine Funktion aus Y
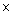 Z in die Potenzmenge über Y Z in die Potenzmenge über Y 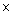 Z Z 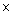 { r, l, o }. { r, l, o }.
(Die im allgemeinen partielle Funktion h mit Tripelmengen als
Funktionswerte kann auch als Relation über Y 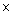 Z Z  Y Y  Z Z  { r, l, o } aufgefaßt werden. r, l, o kennzeichnen die Bewegungsmöglichkeiten
als Ausgabereaktion.) { r, l, o } aufgefaßt werden. r, l, o kennzeichnen die Bewegungsmöglichkeiten
als Ausgabereaktion.)
| Bezeichnungen: |
X |
Eingabealphabet, |
Y |
Bandalphabet, |
| |
Z |
Zustandsmenge, |
F |
Endzustandsmenge, |
| |
z0 |
Anfangszustand, |
# |
Leerfeldsymbol (Blank), |
| |
h |
Überführungsfunktion. |
|
|
-
|
Schematisch kann man einen Turing-Automaten wie folgt darstellen:
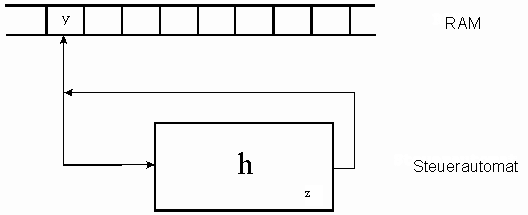
- Bemerkung: Hinsichtlich der Realisierung des Speichers und
seiner Nutzung sind
- noch andere Modellvorstellungen entwickelt worden, z.B. mehrere Speicher
mit verschiedenen Grundalphabeten, andere Adressierungs- bzw.
Bewegungsmöglichkeiten, die im wesentlichen aber keine grundsätzliche
Erweiterungen gegenüber dem obigen Modell darstellen.
Zur Beschreibung
der Arbeitsweise eines Turing-Automaten bei vorgegebener Beschriftung des
Speicherbandes führen wir Konfigurationen als Wörter der Form pzq aus
Y*ZY* ein, wo z den aktuellen Zustand des Steuerautomaten, p die Beschriftung
des Speichers links von der adressierten Zelle, q die Beschriftung des Speichers
ab der adressierten Zelle nach rechts und das erste Zeichen von q den Inhalt der
adressierten Zelle bestimmt. Der Automat arbeitet immer auf einem endlichen
Abschnitt des Speichers und außerhalb dieses Abschnittes ist der Speicher mit
dem Symbol # (Blank) beschriftet.
Alle Konfigurationen #*pzq#* werden mit pzq
identifiziert, d.h., vor p bzw. hinter q dürfen beliebig viele # geschrieben
werden.
Zu einer Konfiguration pzq werden Folgekonfigurationen p´z´q´ als
Verhaltensreaktion des Automaten wie folgt definiert:
Wenn (y, z´, r)  h(x, z) mit q = xw , dann ist p´ = py und q´= w möglich.
h(x, z) mit q = xw , dann ist p´ = py und q´= w möglich.
Wenn (y, z´, l)  h(x, z) mit p = vx´, q = xw, dann ist p´ = v und
q´ = x´yw möglich.
h(x, z) mit p = vx´, q = xw, dann ist p´ = v und
q´ = x´yw möglich.
Wenn (y, z´, o)  h(x, z) mit q = xw , dann ist p´= p und q´= yw möglich.
h(x, z) mit q = xw , dann ist p´= p und q´= yw möglich.
Die
Folgekonfigurationen entstehen durch Anwendung folgender Substitutionsregeln:
| Bei Bewegung |
r |
durch die Regel |
zx  yz´ , yz´ , |
|
| bei |
l |
durch die Regel |
zx  z´y , z´y , |
| und bei |
o |
durch die Regel |
x´zx  z´x´y für beliebige x´ z´x´y für beliebige x´ Y. Y. |
Fassen wir diese Regeln zur Regelmenge RT zusammen, dann kann der Übergang
von der Konfiguration pzq zu einer Folgekonfiguration p´z´q´ wie üblich mit
pzq 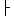 p´z´q´ durch Regelanwendung beschrieben werden,
wobei die Symbole # vor p bzw. hinter q nach Bedarf zu ergänzen sind.
p´z´q´ durch Regelanwendung beschrieben werden,
wobei die Symbole # vor p bzw. hinter q nach Bedarf zu ergänzen sind.
Bezeichnet 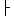 * wieder die reflexiv, transitive Hülle von
* wieder die reflexiv, transitive Hülle von 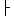 , dann ist die von dem Turing-Automaten akzeptierte
Sprache durch die Wortmenge
, dann ist die von dem Turing-Automaten akzeptierte
Sprache durch die Wortmenge
L ( T ) = { q 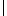 q
q  X* und es existiert ein zf
X* und es existiert ein zf F mit z0q
F mit z0q 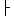 * vzfw }
gegeben.
* vzfw }
gegeben.
Ein Wort q , als Anfangsbeschriftung des Speicherbandes, wird vom
Turing-Automat genau dann akzeptiert, wenn die Konfigurationsfolge zu einem
Endzustand führt. Das Eingabewort q muß dabei nicht notwendig vollständig
gelesen werden. Die Akzeption sagt nichts darüber aus, nach wieviel Schritten
ein Endzustand erreicht wird. Da h allgemein partiell ist, muß nicht zu jeder
Konfiguration eine Folgekonfiguration definiert sein. In diesem Fall sagt man ,
daß der Turing-Automat hält. Wird ein Wort nicht akzeptiert, dann kann
die Konfigurationsfolge unter Umständen unbeschränkt fortsetzbar sein, ohne daß
ein Endzustand angenommen wird oder der Automat anhält.
Modellvarianten :
- Turing-Automaten mit halbseitig unendlichem Speicher
Da der
Automat zu jedem Zeitpunkt nur einen endlichen Speicherbereich benutzt hat,
kann bei notwendigen Bewegungen über das Speicherende vorher eine gegenläufige
Verschiebung des benutzten Speicherbereiches vorgenommen werden. (Auffüllen
mit Blanks.)
- Mehrband-Turing-Automaten
Mehrere Speicherbänder können zu einem
Speicherband mit mehreren Spuren zusammengefaßt werden. Die Zellen des
gemeinsamen Speicherbandes werden entsprechend mit Tupel von Symbolen
beschriftet, die auf den gegebenen Speicherbänder stehen. Zur Festlegung der
jeweils aktuell zu lesenden Zelle wird das dort vorhandene Symbol in der
Beschriftung des gemeinsamen Speicherbandes auf der entsprechenden Spur durch
einen Doppelgänger ersetzt. Diese Doppelgänger sind als neue Symbole in die
Menge Y aufzunehmen. Sobald die jeweilige Zelle nicht mehr aktuell ist, wird
an dieser Stelle auf der entsprechenden Spur wieder das Originalsymbol
eingetragen.
Beide Varianten können daher auf das ursprüngliche Modell des Turing-Automaten
zurückgeführt werden.
 |
- Definition:
Deterministischer Turing-Automat
- Ein Turing-Automat T = ( X, Y, Z, h, z0, F, # ) heißt deterministisch
, falls h eine allgemein partielle Funktion aus Y
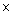 Z in Y Z in Y 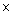 Z Z 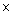 { r, l, o } ist, d.h., { r, l, o } ist, d.h., 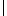 h ( y, z ) h ( y, z ) 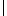 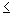 1 für alle y 1 für alle y  Y und z Y und z  Z. Z.
|
|
Satz: Äquivalenz nichtdeterministischer und deterministischer
Turing-Automaten
- Zu jedem nichtdeterministischen Turing-Automaten läßt sich ein deterministischer
Turing-Automat angeben, der dieselbe Sprache akzeptiert.
|
Beweisidee: O.B.d.A. kann von Turing-Automaten mit einem Speicherband
und
- jeweils höchstens zwei möglichen Folgekonfigurationen ausgegangen werden.
Die bildbaren Konfigurationsfolgen können dann als Wörter über einem binären
Alphabet codiert werden. Es wird jetzt ein Dreiband-Automat konstruiert, der
im ersten Band das Eingabewort und im zweiten Band die Kodewörter für die
Konfigurationsfolgen des nichtdeterministischen Automaten speichert. Nachdem
ein Kodewort gespeichert wurde, wird die entsprechende Konfigurationsfolge
auf dem dritten Band deterministisch ausgeführt.
-
| Simulationen |
Turingmaschine 1:
Turingmaschine 2:[start]
|
 |
- Definition:
Aufzählbare (berechenbare) Sprache
- Eine formale Sprache L heißt (rekursiv) aufzählbar , wenn es
einen Turing-Automaten T mit L = L ( T ) gibt , d.h., der L akzeptiert.
|
Beispiel: Der Turing-Automat T=({0, 1}, {0, 1, N, E, #}, {z0,
z1, z2, z3, z4},h, z0,{z4},
#)
- mit h nach Tabelle
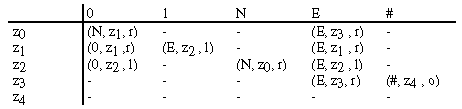
kann in Analogie zu den anderen Automatenbegriffen auch durch den Graphen

festgelegt werden.
Der Automat T akzeptiert die Sprache L (T) = { 0n 1n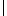 n
n 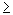 1 }. Dabei bedeuten die Zustände:
1 }. Dabei bedeuten die Zustände:
| z0 |
(Anfangszustand) ersetzt eine rechtsstehende 0 durch N mit Rechtsbewegung. |
| z1 |
sucht nach rechts die erste 1 und ersetzt diese durch E mit Linksbewegung. |
| z2 |
sucht nach links das erste N und geht danach mit Rechtsbewegung
in den Zustand z0. |
| z3 |
sucht nach rechts das erste Blank und geht danach mit Rechtsbewegung
in z4 über. |
| z4 |
(Endzustand) ist der akzeptierende Zustand . |
Zum Eingabewort 0011 entsteht die Konfigurationsfolge z00011 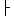 Nz1011
Nz1011 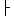 N0z111
N0z111 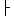 Nz20E1
Nz20E1 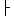 z2N0E1
z2N0E1 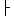 Nz00E1
Nz00E1 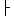 NNz1E1
NNz1E1 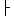 NNEz11
NNEz11 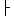 NNz2EE
NNz2EE 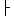 Nz2NEE
Nz2NEE 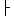 NNz0EE
NNz0EE 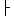 NNEz3E
NNEz3E 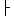 NNEEz3
NNEEz3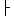 NNEEz4 .
NNEEz4 .
Dieselbe Sprache wird durch den Zweiband-Automaten mit folgendem Graph
akzeptiert.
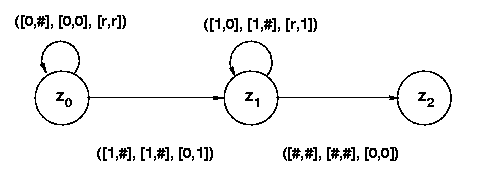
Die Reaktionen auf den beiden Bändern sind jeweils in eckige Klammern gesetzt.
Zunächst schreibt der Automat im Zustand z0 die Nullen vor der ersten
1 vom ersten (Eingabe-)Band auf das zweite Band. Dann wird im Zustand z1
geprüft, ob danach auf dem ersten Band soviele Einsen stehen wie auf dem zweiten
Band Nullen. Nur dann geht der Automat in den akzeptierenden Zustand z2
über.
- Satz: Turing-Automaten und Typ-0 - Sprachen
- Eine formale Sprache L ist genau dann vom Typ-0 , wenn es einen
sie akzeptierenden Turing-Automaten T mit L = L ( T ) gibt.
|
-
- Beweis:
- Konstruktion einer Typ-0 Grammatik G zum Turing-Automaten T mit
L (T) = L (G):
Sei T = (X, Y, Z, h, z0, F, #) und S 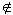 Y
Y 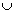 Z. Dann bilden wir M =Y
Z. Dann bilden wir M =Y 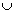 Z
Z 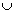 {S} und das zu T gehörige Regelsystem RT , so daß p
{S} und das zu T gehörige Regelsystem RT , so daß p  L (T) genau dann, wenn gilt z0p
L (T) genau dann, wenn gilt z0p 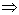 q1zfq2 mit qi
q1zfq2 mit qi Y*, zf
Y*, zf F mit Hilfe der Regeln aus RT (bis auf Blanks).
F mit Hilfe der Regeln aus RT (bis auf Blanks).
Wir bilden die Regelmenge R = RT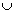 {zf
{zf S, yS
S, yS  S, Sy
S, Sy  S
S 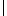 zf
zf F, y
F, y Y}. Dann gilt p
Y}. Dann gilt p  L (T) genau dann, wenn z0p
L (T) genau dann, wenn z0p 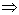 S mit den Regeln aus R. Die Grammatik G´ = (M,
A, R´, S) mit A = X
S mit den Regeln aus R. Die Grammatik G´ = (M,
A, R´, S) mit A = X 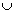 Z
Z 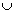 {#} und wo R´ aus R durch Umkehrung der Regeln
entsteht erzeugt dann die Sprache L (G´) mit der Eigenschaft :
{#} und wo R´ aus R durch Umkehrung der Regeln
entsteht erzeugt dann die Sprache L (G´) mit der Eigenschaft :
{ z0p 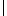 p
p  L (T) } = L (G´)
L (T) } = L (G´) 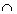 { z0 }A* . Aus G´ kann leicht die gesuchte Grammatik
G mit L (G) = L (T) erzeugt werden.
{ z0 }A* . Aus G´ kann leicht die gesuchte Grammatik
G mit L (G) = L (T) erzeugt werden.
- Konstruktion eines Turing-Automaten T zur Typ-0 Grammatik G mit
L(G)=L (T).
- Idee:Man bilde einen Zweiband-Automat , der auf dem ersten
Band das
- Eingabewort p aufnimmt und damit auf dem zweiten Band die Ableitungen
S
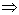 q der Grammatik G bildet. (Die Übergangsfunktion
h des Turing-Automaten entspricht den Regeln der Grammatik, wie eingangs
erläutert.) Danach werden Beschriftungen beider Bänder verglichen.
Der Automat akzeptiert, wenn p = q .
q der Grammatik G bildet. (Die Übergangsfunktion
h des Turing-Automaten entspricht den Regeln der Grammatik, wie eingangs
erläutert.) Danach werden Beschriftungen beider Bänder verglichen.
Der Automat akzeptiert, wenn p = q .
- Folgerungen:
- Eine Sprache ist vom Typ-0 genau dann, wenn sie (rekursiv) aufzählbar
ist.
- Eine Sprache ist (rekursiv)aufzählbar genau dann, wenn sie von einem
deterministischen Turing-Automaten (mit einem Band) akzeptiert wird
 |
Definition: Entscheidbare
Sprachen
- Eine formale Sprache L
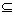 X* heißt (rekursiv) entscheidbar, wenn
es einen deterministischen Turing-Automaten T mit L = L (T) gibt,
der für jede Eingabe X* heißt (rekursiv) entscheidbar, wenn
es einen deterministischen Turing-Automaten T mit L = L (T) gibt,
der für jede Eingabe
p  X* hält . X* hält .
|
| |
-
- Bemerkung: Für solche Sprachen ist durch T ein Entscheidungsverfahren
gegeben,
- mit dem für jedes Wort aus X* festgestellt werden kann, ob es zu L gehört
oder nicht. Diese Entscheidung kann am Zustand, den T nach dem Anhalten einnimmt,
abgelesen werden. In jedem Fall erreicht der Turing-Automat T eine Konfiguration,
zu der keine Folgekonfiguration existiert.
-
|
Satz: Zusammenhang zwischen aufzählbaren und
entscheidbaren Sprachen. Eine Sprache L 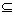 X* ist genau dann entscheidbar, wenn L und ihr
Komplement X* ist genau dann entscheidbar, wenn L und ihr
Komplement
X* \ L aufzählbar ist.
|
-
- Beweisidee:
- Nach Definition ist L
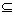 X* genau dann entscheidbar, wenn ihr Komplement
X* \ L entscheidbar ist. Jede entscheidbare Sprache ist aber auch aufzählbar.
X* genau dann entscheidbar, wenn ihr Komplement
X* \ L entscheidbar ist. Jede entscheidbare Sprache ist aber auch aufzählbar.
- Wenn L und X* \ L aufzählbar sind, dann existieren Turing-Automaten
T und T´ mit L (T) = L und L (T´) = X* \ L . Man bilde einen Turing-Automaten
mit zwei Bändern, der auf dem ersten Band den Automaten T und auf dem
zweiten Band den Automaten T´ simuliert bei dem gleichen Eingabewort
p  X*. Die Zustände dieses Automaten sind die Zustandspaare
der Automaten T und T´. Der Automat soll anhalten (keine Folgekonfiguration
definiert), sobald bei einem der Automaten T oder T´ein Endzustand ereicht
wird. Das Wort p wird akzeptiert, wenn der Automat auf Band eins anhält,
d.h., wenn T anhält.
X*. Die Zustände dieses Automaten sind die Zustandspaare
der Automaten T und T´. Der Automat soll anhalten (keine Folgekonfiguration
definiert), sobald bei einem der Automaten T oder T´ein Endzustand ereicht
wird. Das Wort p wird akzeptiert, wenn der Automat auf Band eins anhält,
d.h., wenn T anhält.
-
|
Satz: Existenz nicht entscheidbarer Sprachen
Es existieren (rekursiv) aufzählbare Sprachen, die nicht entscheidbar
sind.
|
- Beweisidee:
- Jede endliche algebraische Struktur kann über einem zweielementigen Alphabet
{0, 1} kodiert werden, d.h., man kann eine injektive Funktion
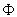 angeben, die zu jeder Struktur eindeutig eine Folge
(Kodewort) über {0, 1} bestimmt, aus der umgekehrt auch die kodierte Struktur
wieder ermittelt werden kann. Die Werte von
angeben, die zu jeder Struktur eindeutig eine Folge
(Kodewort) über {0, 1} bestimmt, aus der umgekehrt auch die kodierte Struktur
wieder ermittelt werden kann. Die Werte von 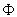 und
und 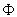 -1 sind effektiv zu konstruieren. Entsprechendes gilt
für Tupel aus (endlichen) Wörtern und Strukturen.Sei
-1 sind effektiv zu konstruieren. Entsprechendes gilt
für Tupel aus (endlichen) Wörtern und Strukturen.Sei 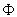 eine solche Kodierungs-funktion der Paare (p, T),
wo p
eine solche Kodierungs-funktion der Paare (p, T),
wo p  X* und T Turing-Automat über X.
X* und T Turing-Automat über X.
Wir führen die (Universal)-Sprache Lu = { 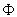 (p, T)
(p, T) 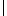 p
p  L (T) }
L (T) } 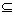 {0, 1}* ein. Lu ist (rekursiv) aufzählbar und wird durch
einen Zweiband-Automaten Tu akzeptiert, der auf dem ersten Band
zur Eingabe
{0, 1}* ein. Lu ist (rekursiv) aufzählbar und wird durch
einen Zweiband-Automaten Tu akzeptiert, der auf dem ersten Band
zur Eingabe 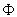 (p, T) entsprechend
(p, T) entsprechend 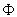 -1 zunächst p und T bestimmt und danach
auf dem zweiten Band den Automaten T bei der Eingabe p simuliert. Tu
akzeptiert
-1 zunächst p und T bestimmt und danach
auf dem zweiten Band den Automaten T bei der Eingabe p simuliert. Tu
akzeptiert 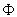 (p, T), wenn p von T akzeptiert wird. Tu heißt Universal-Automat
, da er beliebige T simuliert.
(p, T), wenn p von T akzeptiert wird. Tu heißt Universal-Automat
, da er beliebige T simuliert.
Andererseits ist die (Diagonal)-Sprache Ld = { 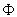 ´(T)
´(T) 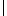
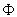 ´(T)
´(T) 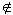 L (T) }
L (T) } 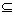
{0, 1}* , wo 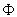 ´(T) Kodewort von T, nicht aufzählbar, denn sonst müßte es einen Turing-Automaten
Td mit L (Td) = L geben,
wofür
´(T) Kodewort von T, nicht aufzählbar, denn sonst müßte es einen Turing-Automaten
Td mit L (Td) = L geben,
wofür 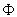 ´(Td)
´(Td)  Ld =
Ld =
L (Td) genau dann, wenn 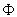 ´(Td)
´(Td) 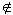 L (Td) ist.
L (Td) ist.
Wäre nun {0, 1}* \ Lu aufzählbar, dann könnten wir Ld
dadurch aufzählen, daß wir durch einen Turing-Automaten für die Eingabe 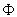 ´(T) das Kodewort
´(T) das Kodewort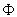 (
(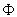 ´(T), T) erzeugen und akzeptieren, wenn dieses Wort
nicht zu Lu gehört. Wenn aber {0, 1}* \ Lu nicht aufzählbar
ist, dann kann die durch Tu aufzählbare Sprache Lu auch
nicht entscheidbar sein.
´(T), T) erzeugen und akzeptieren, wenn dieses Wort
nicht zu Lu gehört. Wenn aber {0, 1}* \ Lu nicht aufzählbar
ist, dann kann die durch Tu aufzählbare Sprache Lu auch
nicht entscheidbar sein.
- Folgerung:
- Die aufzählbaren Sprachen sind nicht abgeschlossen gegen Komplementbildung.
 |
- Defintion:
Turing-berechenbare Funktion
- Sei T ein deterministischer Zweiband-Automat mit dem Alphabet X1
für das erste (Eingabe)-Band und X2 für das zweite (Ausgabe)-Band.
fT bezeichne die Funktion , die genau für diejenigen Wörter
p über X1 definiert ist, für die T mit p als Beschriftung
des Eingabebandes anhält, und der Funktionswert fT(p) als
Beschriftung des Ausgabebandes entsteht.
Eine Funktion f aus X1* nach X*
heißt (Turing)-berechenbar, wenn es einen deterministischen Turing-Automaten
T mit fT = f gibt.
|
Eigenschaften:
- 1. Jede im intuitiven Sinne berechenbare Funktion ist Turing-berechenbar.
2. Es gibt Funktionen, die nicht Turing-berechenbar sind.
 |
Definition: Turing-erzeugbare
Sprache
- Sei T ein nichtdeterministischer Mehrband-Automat mit einem (Ausgabe)-Band,
auf dem nur von links nach rechts geschrieben werden kann. Mit ERZ(T)
bezeichnen wir die Menge aller Inschriften dieses Ausgabebandes ohne
Blanks, die entstehen, wenn T angesetzt auf leere Bänder anhält.
Eine Sprache L heißt Turing-erzeugbar, wenn es einen nichtdeterministischen
Turing-Automaten T mit ERZ(T) = L gibt.
-
|
-
- Eigenschaften:
- Jede Turing-erzeugbare Sprache ist (rekursiv)aufzählbar und umgekehrt.
- Wenn L aufzählbar, dann gibt es einen Turing-Automaten der jedes Wort
von L genau einmal erzeugt.
- L ist genau dann entscheidbar, wenn es einen Turing-Automaten gibt,
der die Wörter von L in aufsteigender Länge und genau einmal erzeugt.
-
 |
Definition: (rekursiv)
reduzierbare Sprachen
Eine Sprache L1 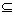 X1* heißt auf die Sprache L2 X1* heißt auf die Sprache L2 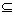 X2* (rekursiv) reduzierbar X2* (rekursiv) reduzierbar
(L1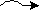 L2), wenn es eine überall auf X1* definierte
Turing-berechenbare Funktion f nach X2* gibt, für die f(p) L2), wenn es eine überall auf X1* definierte
Turing-berechenbare Funktion f nach X2* gibt, für die f(p)  L2 genau dann gilt, wenn p L2 genau dann gilt, wenn p  L1. L1. |
Eigenschaften:
- Die Relation
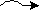 ist reflexiv und transitiv.
ist reflexiv und transitiv.
- L1
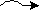 L2 genau dann, wenn X1* \ L1
L2 genau dann, wenn X1* \ L1 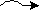 X2* \ L2.
X2* \ L2.
- Wenn L1
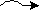 L2 gilt und L2 ist aufzählbar, dann ist auch
L1 aufzählbar.
L2 gilt und L2 ist aufzählbar, dann ist auch
L1 aufzählbar.
- L ist genau dann aufzählbar, wenn L
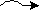 Lu mit Lu (Universal)-Sprache.
Lu mit Lu (Universal)-Sprache.
 |
- Definition:
Eigenschaften P aufzählbarer Sprachen sind Teilklassen
der Klasse L0
- der Typ-0 Sprachen, d.h., Prädikate über L0. Eine Eigenschaft
P heißt nicht-trivial, wenn P mindestens eine und nicht alle
Sprachen aus L0 umfaßt, d.h.,
es gilt: 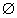 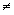 P P 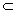 L0. L0.
|
|
Satz: Existenz nicht entscheidbarer Eigenschaften
aufzählbarer Sprachen (Satz von Rice)
- Jede nicht-triviale Eigenschaft aufzählbarer Sprachen ist unentscheidbar.
|
- Beweisidee:
- L sei eine aufzählbare Sprache mit L = L (T) und P sei eine nicht-triviale
Eigenschaft aufzählbarer Sprachen , die auf L aber nicht auf
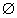 zutrifft, d.h.,
zutrifft, d.h.,
L  P und
P und 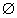
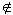 P. Eine solche Eigenschaft P existiert, da P entscheidbar genau dann,
wenn (nicht P ) entscheidbar ist.
P. Eine solche Eigenschaft P existiert, da P entscheidbar genau dann,
wenn (nicht P ) entscheidbar ist.
Zu einem Wort q über dem Eingabealphabet von T konstruieren wir einen Turing-Automaten
Tq der bei einem Wort p als Beschriftung des (Eingabe)Bandes genau
dann anhält , wenn der Automat T bei p und der Automat Tu bei q
anhält, d.h., es gilt :
L (Tq) = { p 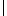 p
p  L und q
L und q  L (Tu) = Lu }.
Also ist L (Tq) = L , falls q
L (Tu) = Lu }.
Also ist L (Tq) = L , falls q  Lu und L (Tq) =
Lu und L (Tq) = 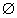 , falls q
, falls q 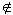 Lu.
Lu.
Das bedeutet : L (Tq)  P genau dann, wenn q
P genau dann, wenn q  Lu.
Lu.
Sei Lp = {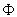 ´(T)
´(T) 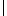
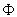 ´(T) Kodewort des Turing-Automaten T und L(T)
´(T) Kodewort des Turing-Automaten T und L(T)  P}. Wäre Lp entscheidbar, dann wäre auch entscheidbar,
ob L(Tq)
P}. Wäre Lp entscheidbar, dann wäre auch entscheidbar,
ob L(Tq)  P gilt oder nicht. Damit wäre aber im Widerspruch zu früher Lu
entscheidbar. Also kann Lp nicht entscheidbar sein. Damit ist auch
die nicht-triviale Eigenschaft P nicht entscheidbar.
P gilt oder nicht. Damit wäre aber im Widerspruch zu früher Lu
entscheidbar. Also kann Lp nicht entscheidbar sein. Damit ist auch
die nicht-triviale Eigenschaft P nicht entscheidbar.
- Folgerung: Es ist nicht entscheidbar, ob eine beliebige (rekursiv)
aufzählbare
- (Typ-0) Sprache leer, bzw. endlich, bzw. regulär, bzw. kontextfrei, bzw.
kontextabhängig, bzw. entscheidbar ist. (Nicht-triviale Eigenschaften)
- Bemerkungen:
- Folgende Eigenschaften (rekursiv) aufzählbarer Sprachen L sind nicht
(rekursiv) aufzählbar: L =
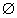 ; L = X* ; L rekursiv-aufzählbar ; L nicht rekursiv-aufzählbar
; L regulär ; L \ Lu
; L = X* ; L rekursiv-aufzählbar ; L nicht rekursiv-aufzählbar
; L regulär ; L \ Lu 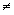
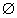 .
.
- Folgende Eigenschaften (rekursiv) aufzählbarer Sprachen sind (rekursiv)
aufzählbar : L
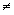
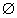 ;
; 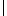 L
L 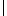
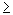 k > 0 ; p
k > 0 ; p  L für ein vorgegebenes festes
L für ein vorgegebenes festes
p X* ; L
X* ; L 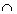 Lu
Lu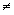
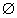 .
.
- Es ist nicht entscheidbar, ob ein (beliebiger) Turing-Automat bei leerem
Eingabeband (nur Blanks) hält. (Halteproblem: Verallgemeinerung des Satzes
von Rice)
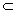 Y, Y
Y, Y 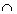 Z =
Z = 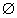 , #
, #  Y \ X ,
Y \ X ,  Z, F
Z, F 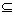 Z und
Z und
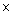 Z in die Potenzmenge über Y
Z in die Potenzmenge über Y 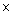 Z
Z 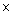 { r, l, o }.
{ r, l, o }. 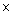 Z
Z 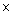 Y
Y 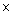 Z
Z 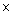 { r, l, o } aufgefaßt werden. r, l, o kennzeichnen die Bewegungsmöglichkeiten
als Ausgabereaktion.)
{ r, l, o } aufgefaßt werden. r, l, o kennzeichnen die Bewegungsmöglichkeiten
als Ausgabereaktion.)
 p´z´q´ durch Regelanwendung beschrieben werden,
wobei die Symbole # vor p bzw. hinter q nach Bedarf zu ergänzen sind.
p´z´q´ durch Regelanwendung beschrieben werden,
wobei die Symbole # vor p bzw. hinter q nach Bedarf zu ergänzen sind.
 q
q 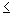 1 für alle y
1 für alle y 
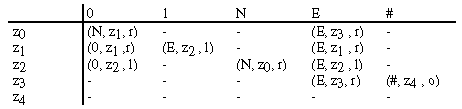

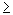 1 }. Dabei bedeuten die Zustände:
1 }. Dabei bedeuten die Zustände:

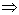 q1zfq2 mit qi
q1zfq2 mit qi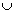 Z
Z 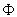 angeben, die zu jeder Struktur eindeutig eine Folge
(Kodewort) über {0, 1} bestimmt, aus der umgekehrt auch die kodierte Struktur
wieder ermittelt werden kann. Die Werte von
angeben, die zu jeder Struktur eindeutig eine Folge
(Kodewort) über {0, 1} bestimmt, aus der umgekehrt auch die kodierte Struktur
wieder ermittelt werden kann. Die Werte von  P
P