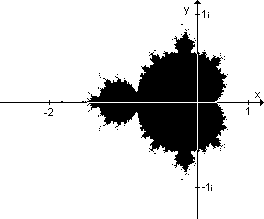Die Mandelbrotmenge

Für diesen Abschnitt werden Kenntnisse mit komplexen Zahlen empfohlen.

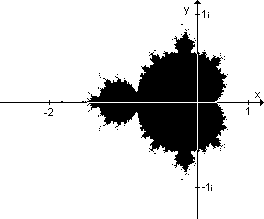Dies ist die grafische Darstellung der Mandelbrotmenge. Sie besteht aus komplexen Zahlen, die alle ein bestimmtes Kriterium erfüllen. Deshalb wird die Mandelbrotmenge in einer "komplexen Ebene" dargestellt: die x-Achse entspricht dem Real-Teil einer komplexen Zahl; die y-Achse dem Imaginärteil. Man durchläuft der Reihe nach viele Punkte innerhalb der komplexen Ebene und prüft, ob sie innerhalb der Mandelbrotmenge liegen. Es gibt also vorerst nur zwei Arten von Punkten: die einen Punkte liegen nicht in der Menge und werden nicht gefärbt. Die anderen liegen innerhalb der Menge und erhalten zum Beispiel die Farbe Schwarz.

Wie findet man nun heraus, ob die Punkte in der Mandelbrotmenge liegen ?

Man wählt einen Punkt C aus der komplexen Ebene. C ist nun eine komplexe Zahl, mit dem Realteil als x-Koordinate und dem Imaginärteil als y-Koordinate: c = x + i*y.

Die folgende Formel wird nun immer wieder auf Z angewendet:

Man nennt diesen Vorgang eine "Iteration": die Formel wird wiederholt angewendet. Wir beginnen mit Z₀=0. Z₁ erhält somit den Wert C. Das ganze beginnt von neuem: das "neue" Z (Z_n) erhält nun den Wert des "alten" Z (Z_n-1) zum Quadrat plus C.

Dieser Vorgang kann natürlich nicht unendlich lange wiederholt werden. Nach beispielsweise 20 Iterationen wird der Vorgang abgebrochen. Ist nun der Betrag von Z₂₀ kleiner als 2, so nimmt man an, dass der Punkt C innerhalb der Mandelbrotmenge liegt. Überschreitet der Betrag den Wert 2, so nimmt man an, dass der Punkt außerhalb der Menge liegt und man kann die Iteration schon früher abbrechen.

Wie kommen die Farben zustande ?

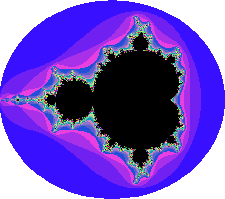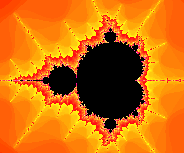
An für sich sieht die Mandelbrotmenge einfarbig aus. Es ist möglich, den Punkten außerhalb der Mandelbrotmenge Farben zuzuweisen. Sie liegen alle außerhalb der Mandelbrotmenge, das heißt, die Iterationsschleife konnte schon früher abgebrochen werden. Die Farbe der Punkte ist nun abhängig von den Iterationen, die der Computer benötigt hat, um herauszufinden, dass sie außerhalb der Menge liegen. Im Bild links wurde den verschiedenen Iterationsbereichen je eine Farbe zugeordnet. Ganz außen um die Mandelbrotmenge erstreckt sich ein blauer Kreis. Der Computer benötigte für die Punkte in dieser Zone nur eine Iteration, um herauszufinden, dass die Punkte nicht in der Menge liegen. Es folgen Abstufungen von violett: der Computer benötigte erst zwei, dann drei Iterationen, usw. Die Punkte im schwarzen Bereich liegen innerhalb der Mandelbrotmenge. Hier benötigte der Computer alle Iterationen, weil die Schleife nicht vorher abgebrochen werden konnte: der Betrag war nie größer als zwei.

Vergrößerung

Eine Mandelbrotmenge kann beliebig stark vergrößert werden. Man muss jedoch beachten, die Iterationszahl höher zu setzen, sonst erreicht man bald gewisse Grenzen. Durch die Erhöhung kann die feine Struktur am Rand der Mandelbrotmenge untersucht werden.

Ein Bereich der Mandelbrotmenge wurde vergrößert: Links wurde die vorgegebene Anzahl von 20 Iterationen beibehalten. Beim mittleren Bild wurde die Anzahl auf 100 Iterationen erhöht: der Ausschnitt ist nun wesentlich komplexer.

Man sollte jedoch immer eines im Kopf behalten: je höher die Iterationszahl, desto höher wird die Rechenzeit des Computers. Dies lässt sich besonders gut am schwarzen Bereich der Mandelbrotmenge demonstrieren. Der Computer benötigt dort immer die maximale Anzahl an Iterationen. Man muss deshalb abwägen: will man die Menge sehr schnell oder sehr gut darstellen? Beides zusammen könnte bei diesem Rechenverfahren ein Problem ergeben.

Flächeninhalt einer Darstellung der Mandelbrotmenge

Die Bestimmung eines Näherungswertes für den Flächeninhalt einer Darstellung der Mandelbrotmenge über die Monte-Carlo-Methode ist relativ einfach: Man zählt einfach die Punkte, die schwarz gefärbt sind und teilt sie durch die Gesamtpixel, die auf dem Bildschirm dargestellt werden. Multipliziert man den erhaltenen Wert mit 100, so erhält man die prozentuale Wahrscheinlichkeit, mit der die Punkte in den Kreis fallen. Die Genauigkeit des Näherungswertes für den Flächeninhalt hängt von der Anzahl der Iterationen ab. In der folgenden Tabelle sind die berechneten Näherungswerte für den Flächeninhalt im Verhältnis zu den verwendeten Iterationen dargestellt:

Am Anfang, bei 0 Iterationen, ist die Wahrscheinlichkeit, mit der die Punkte in die Mandelbrotmenge fallen, gleich 100%; denn bei Null Iterationen rechnet der Computer einfach alle Punkte zur Mandelbrotmenge. Je mehr Iterationen verwendet werden, desto klarer wird die Form und desto genauer wird der Flächeninhalt:

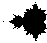1 Iteration	2	3	4	5	6	7	8	9

Julia-Mengen

Julia-Mengen werden fast genauso berechnet wie die Mandelbrotmenge:

Der Unterschied zur Berechnung der Mandelbrotmenge ist, dass der Punkt C hier für jeden Punkt der komplexen Ebene konstant bleibt. Z erhält nun die Koordinaten eines beliebigen Punktes auf der komplexen Ebene, während C für bei der Berechnung aller Punkte gleich bleibt. C ist auch hier eine komplexe Zahl und kann ebenfalls einen beliebigen Punkt auf der komplexen Ebene darstellen; muss aber bei allen Berechnungen der Punkte der zukünftigen Juliamenge den gleichen Wert haben; darf sich also nie ändern. Da C beliebige Koordinaten besitzen kann, ist jedem Punkt der komplexen Ebene eine eigene Juliamenge zugeordnet - und dadurch auch jedem Punkt der Mandelbrotmenge.

Mandelbrot Calculator

Version 3.1: ab Windows 95:
Berechnet und zeichnet Mandelbrot- und Juliamengen; errechnet mit Hilfe der Monte-Carlo-Methode den Flächeninhalt der dargestellten Mengen

Quellcode herunterladen (C++-Quellcode; WinAPI)
Programm herunterladen (.zip-Datei, Windows)

Eine sehr gute Website über die Julia- und Mandelbrotmenge ist Fabio Cesaris Fractal Explorer.

Mathe-Startseite